#14：塔勒布新书《肥尾效应》导读（Sarah & 戴国晨）
01:46:10 Share

欢迎各位收听 Traders' Talk 第 14 期。在本期播客中，我请到了《肥尾效应》的译者戴国晨作为本期节目的嘉宾，一起对塔勒布的新书《肥尾效应》尝试做一期音频导读。我们探讨了书中的核心概念，也尽量穿插了一些有趣的例子，最后也聊了聊塔勒布本人的鲜明个性。

欢迎各位收听后在评论区里写下对本期节目的感想，我将挑选出 3 个优质评论的听众分别赠予《肥尾效应》一本。此外，我在评论区置顶链接里放上了中信出版社给的优惠购买链接，也欢迎各位对这本书感兴趣的朋友前往购买。

希望各位收听愉快~

       

【嘉宾介绍】

戴国晨，

- 塔勒布新书《肥尾效应》译者

- 中国人民大学物理学学士，美国纽约大学金融工程硕士

- 曾任职多伦多道明银行（纽约）销售和交易部门，现就职于上海艾方资产反脆弱投资部，从事海内外尾部风险管理研究

【本期播客大纲】

一、综述《肥尾效应》主旨

二、关于分布的类型和性质

三、关于肥尾参数的估计

四、补充几个有趣的例子

五、关于黑天鹅

六、其他

【Timeline & Key Point】

一、综述《肥尾效应》

00:04:38 本书结构

00:06:17 本书主旨

“本书主要讲述产生极端事件的统计分布类型，以及在这类分布下如何进行统计推断和做出决策。现有的大多数“标准”统计理论均来自薄尾分布，它们应用于肥尾的过程中需要经过渐进性调整，这往往不是小改动，原理论可能会被完全舍弃。”——引用自《肥尾效应》第一章序言

00:09:47 本期播客结构——面对随机性事件，人们可能面对的风险有如下几种：

- 不知道分布的类型和性质

- 知道分布的类型和性质，错误地估计了参数

- 黑天鹅

二、关于分布的类型和性质

（一）关于肥尾

00:10:43 具体有哪些分布类型

- 退化分布：只有一种结果，不存在随机性

- 伯努利分布（离散型的0-1分布）：只有两种可能的结果

- 自然正态分布（允许出现正负无穷）：自然现象的分布

- 随机游走中求和而来的正态分布（没法到无穷大）

- 亚指数分布（介于正态分布和幂律分布之间）：包含对数正态分布（方差小的时候属于薄尾分布，方差大的时候属于厚尾分布）

- 幂律分布

肥尾之母、超级肥尾：对数帕累托分布 （书 5.5 章节）

00:13:40 厚尾 vs 肥尾

- 厚尾或重尾 (Thick/Heavy Tail)：比正态分布峰度更高的分布

- 肥尾 (Fat Tail) ：极端厚尾/幂律尾类分布

（二）关于正态分布

00:15:20 正态分布的定义与性质

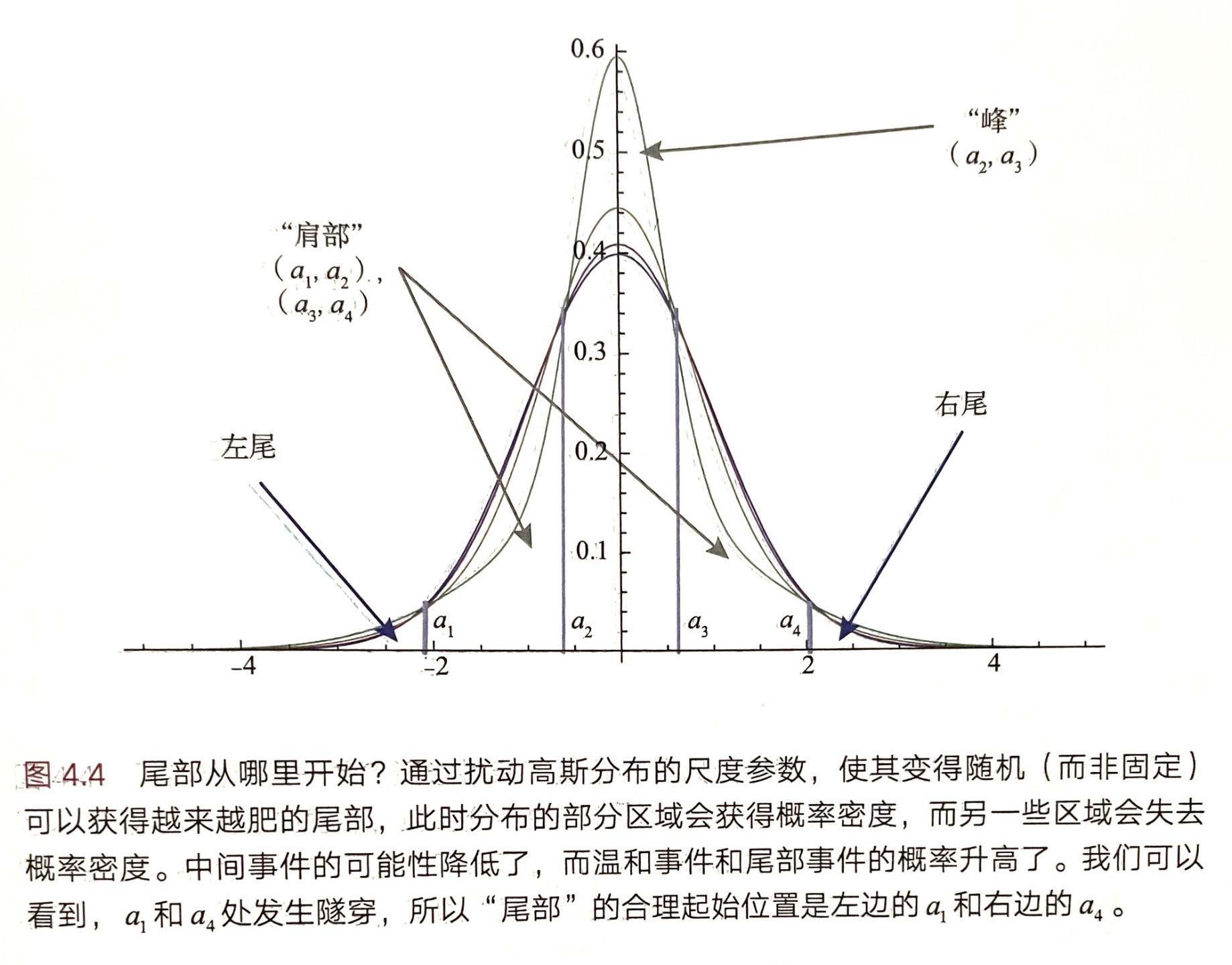
钟型曲线，分为躯干、肩部和尾部（头肩尾），凸-凹-凸结构

- 衡量参数：μ（均值）和 σ（方差），μ = 0,σ = 1 的正态分布是标准正态分布

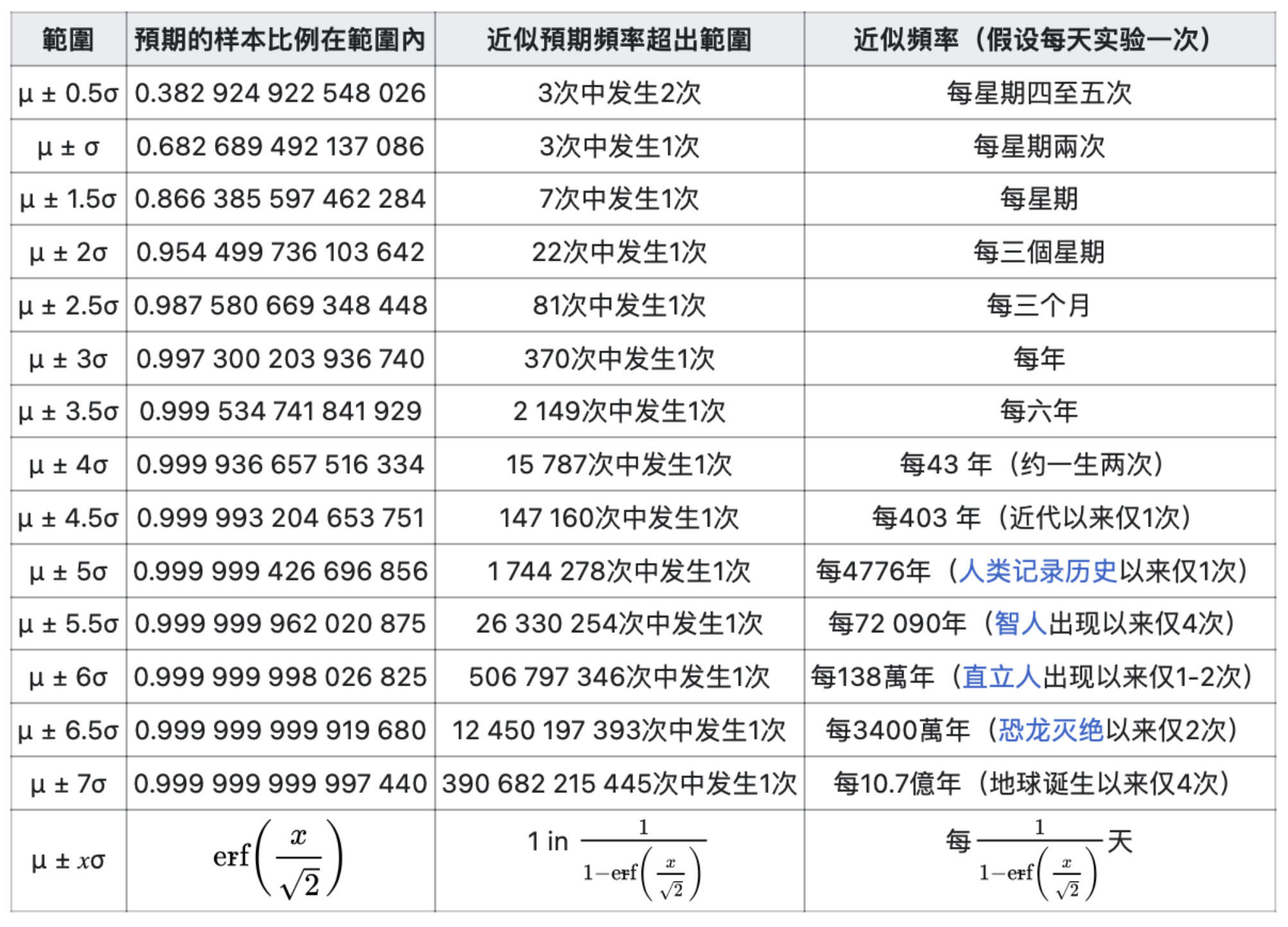
- 3σ定律（three-sigma rule）/68-95-99.7 原则：“几乎所有”的值都在平均值正负三个标准差的范围内（实验上可以将99.73%的机率视为“几乎一定”）

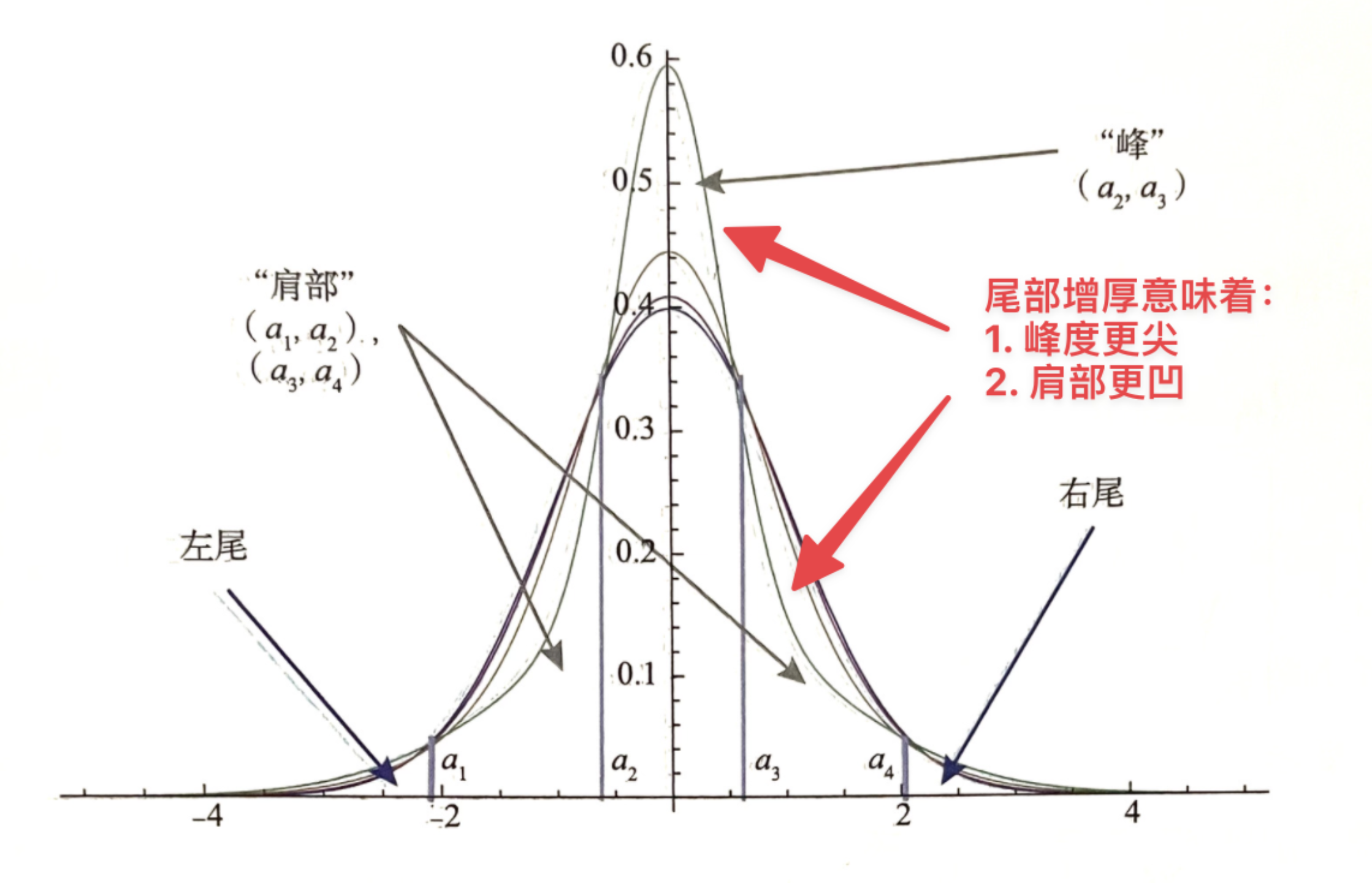
00:22:10 尾部增厚意味峰度更尖、肩部更凹 ###

（三）关于矩

00:26:16 从矩的角度看不同分布

各阶矩的含义：

- 零阶矩：总概率

- 一阶矩：均值，即数学期望值

- 二阶矩：方差，衡量数据的离散程度

- 三阶矩：偏度，衡量随机密度函数向左或向右偏的程度

- 四阶矩：峰度，衡量峰部有多尖

从矩的角度看不同分布：

- 正态分布：衡量参数为一阶矩μ（均值）和二阶矩 σ（方差），三阶矩偏度为 0，四阶矩峰度为 3（嘉宾说的峰度为 0 其实指的是超额峰度，只不过一般习惯对峰度做-3 处理）

- 入门级厚尾分布：各种矩都是有限的数，峰度比正态略大

- 亚指数分布：高阶矩开始退化

- 幂律分布：高阶矩继续退化，直至所有的矩完全消失

（四）关于平均斯坦与极端斯坦

00:30:55 平均斯坦与极端斯坦（对应书中的 3.1 章节）

区分点：随机变量连续两次大于 X 的概率跟单次大于 2X 的概率，平均斯坦是前者大于后者，极端斯坦则是后者大于前者。

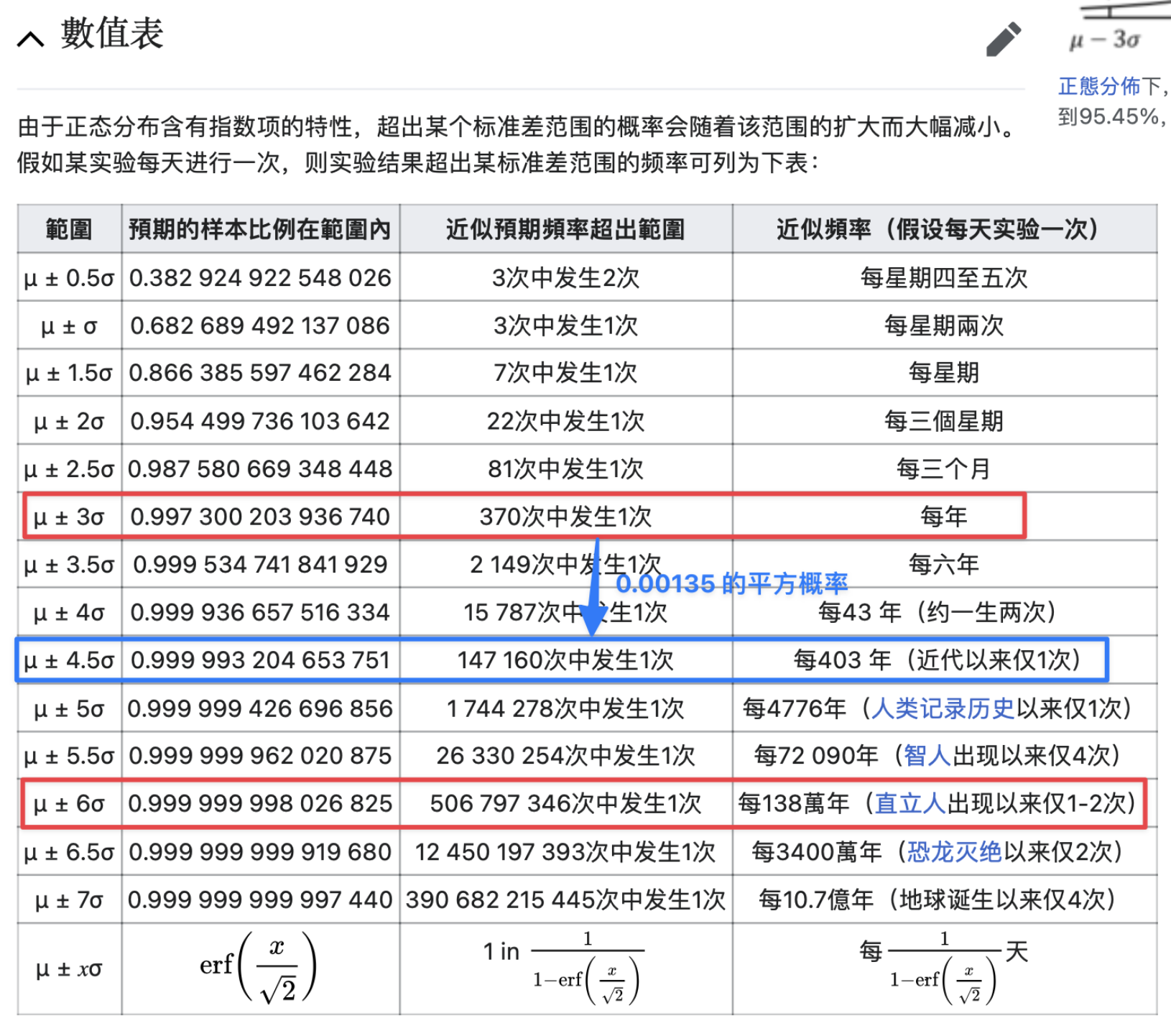
对于正态分布这种薄尾分布来说，出现一次 3σ 事件的概率是 0.00135（非双尾分布）。假设每天实验一次，连续两次出现 3σ 事件的概率是 1.8 x 10 的负六次方，大约是每 403 年，这会远大于出现一次 6σ 事件的概率，大约是直立人出现以来仅 1-2 次（见下方数值表）。 00:37:45 破产更可能来自某次极端事件而不是一系列糟糕事件的累积（对应书中 3.1 及 3.4.2 章节例子）

00:39:32 保险只能在平均斯坦中起作用，在存在巨灾风险的情况下，永远不要出售一种损失无上限的保险，这一点被称为灾难原则（书 3.1 章节）

00:40:37 通过设定历史最高水位去设定安全水位线的例子（书 3.4 效应五）

（五）关于幂律分布

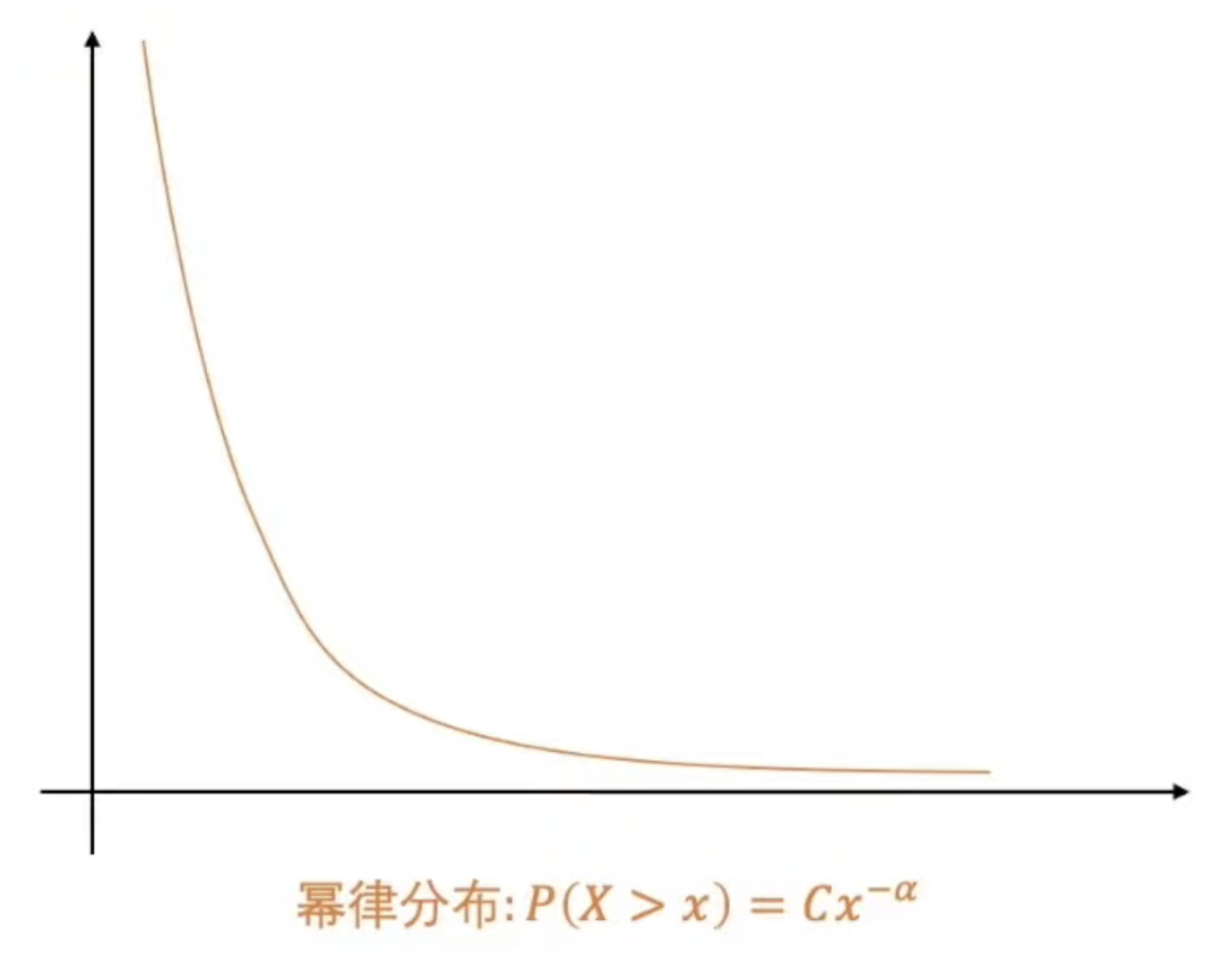
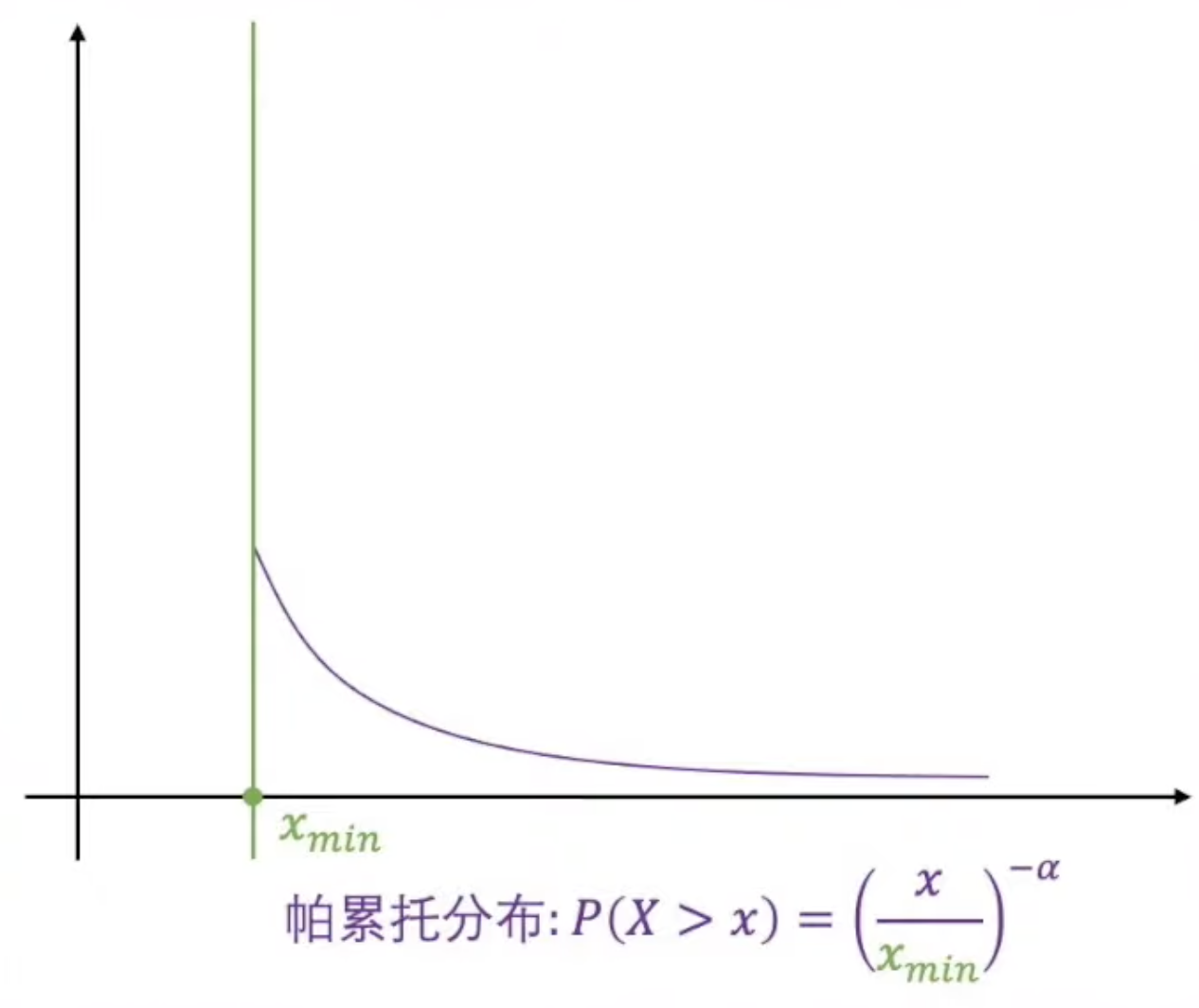
00:42:08 幂律曲线与帕累托分布的关系

帕累托分布，即我们熟知的二八法则、马太效应。它最受关注的性质就是右边这个长长的尾巴，尾巴速度下降慢，就能带来很多特别的性质。 ## 三、关于肥尾参数的估计

00:45:42 知道了分布的类型，接下来需要估计哪些参数

（一）样本量

00:47:58 肥尾分布会极大地增加求解统计量的样本量要求

帕累托分布中98% 的样本都会小于均值，而剩下的 2%对整体的均值几乎起到确定性的作用，所以几乎可以把绝大部分的样本当作噪声。

00:48:41 帕累托80/20分布需要比正态分布多出 10 的 9 次方量级的样本量才能达到类似的精确度（书中第八章【需要多少数据？肥尾的定量衡量方法】）

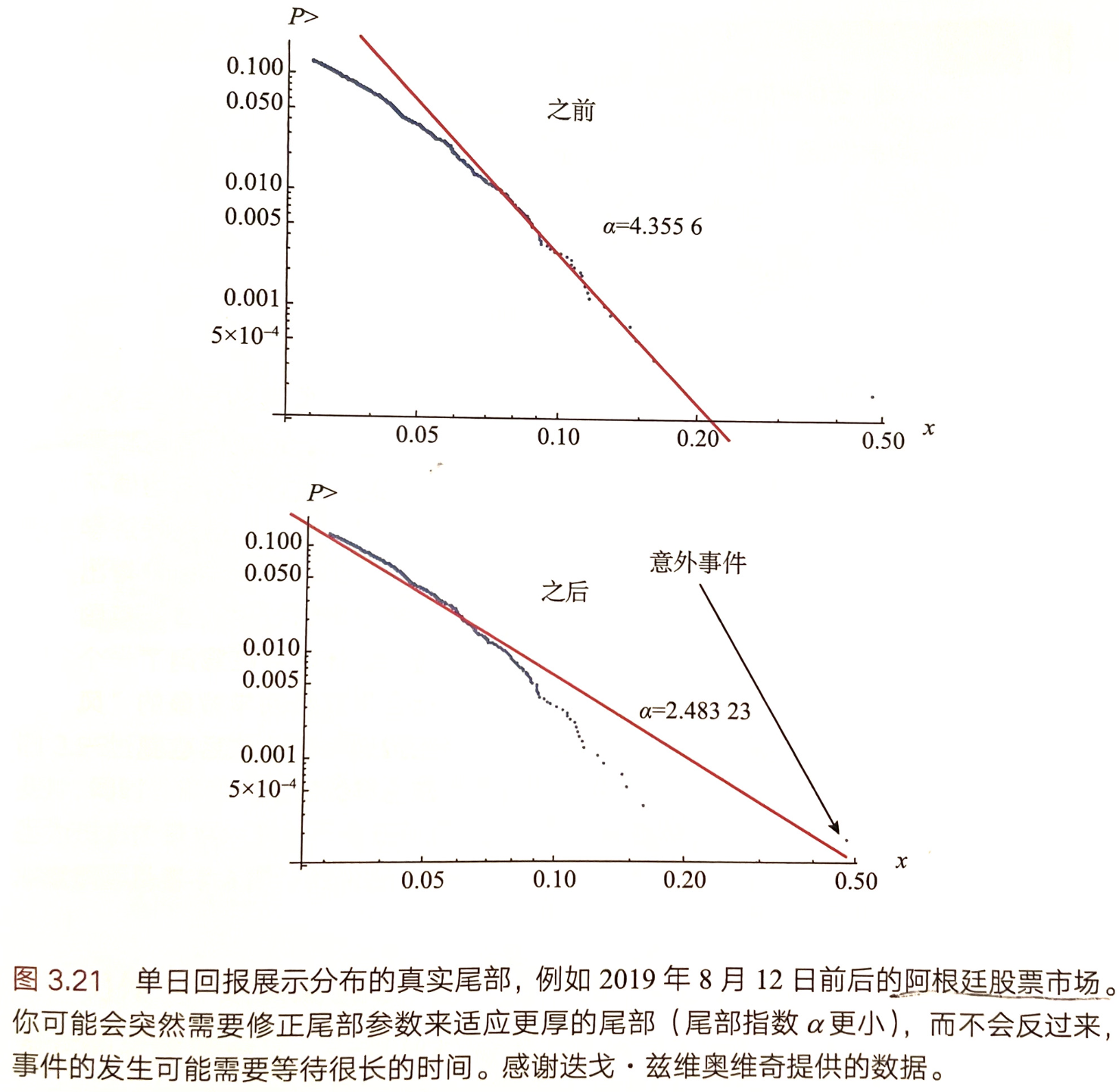
00:50:00 阿根廷股市的例子（书 3.5 章节）

###

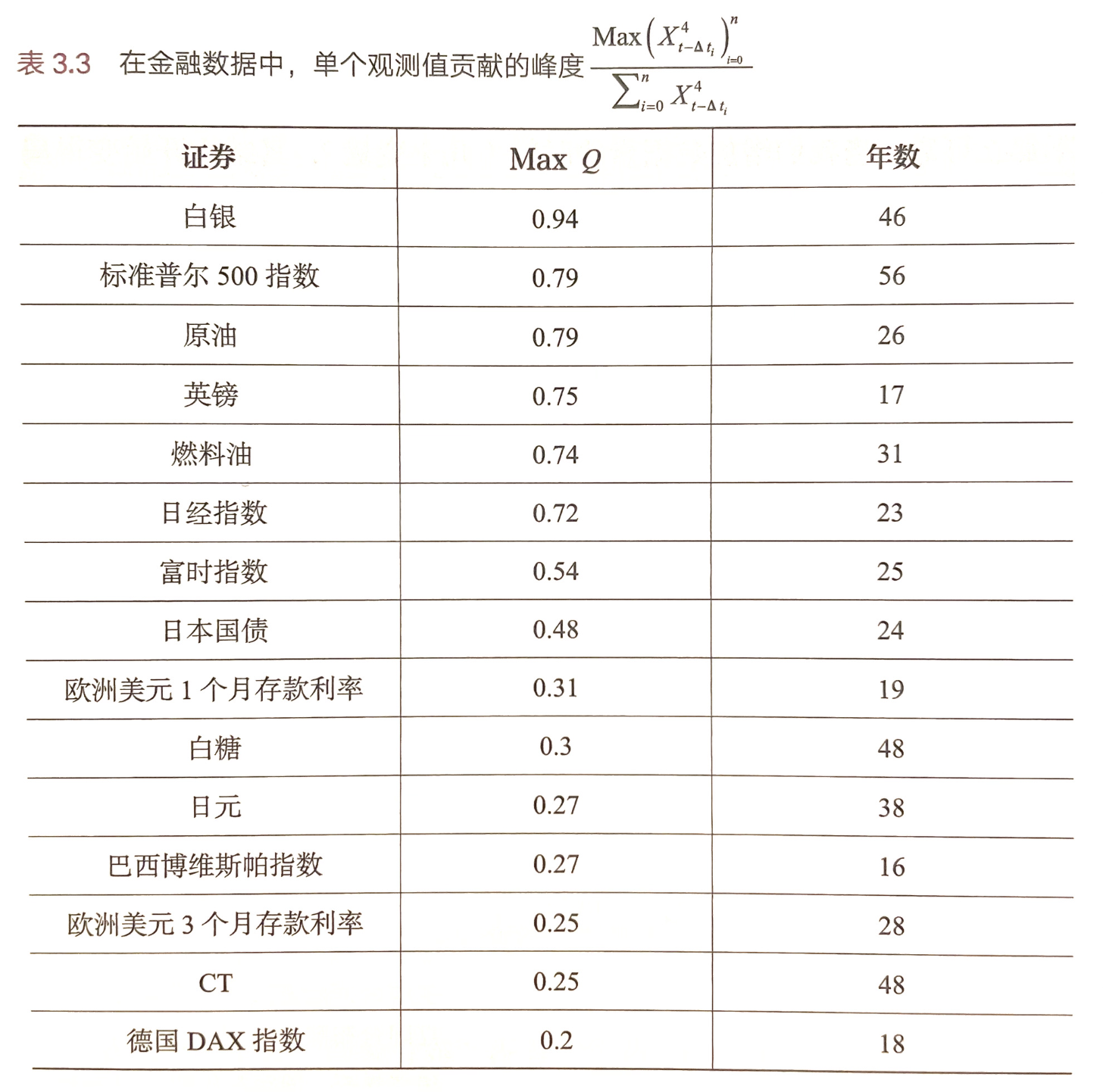
（二）单个观测值贡献的峰度

00:51:12 回测了 4 万多种证券，单个观测值贡献的峰度都非常高（如下图），无一例外全部符合肥尾分布（书 3.7 章节） 00:52:35  为什么马科维茨投资组合分散化配置方法不是最佳方式（书 8.5 章节）

（三）大数定律及中心极限定理

00:55:44 大数定律与中心极限定理的定义

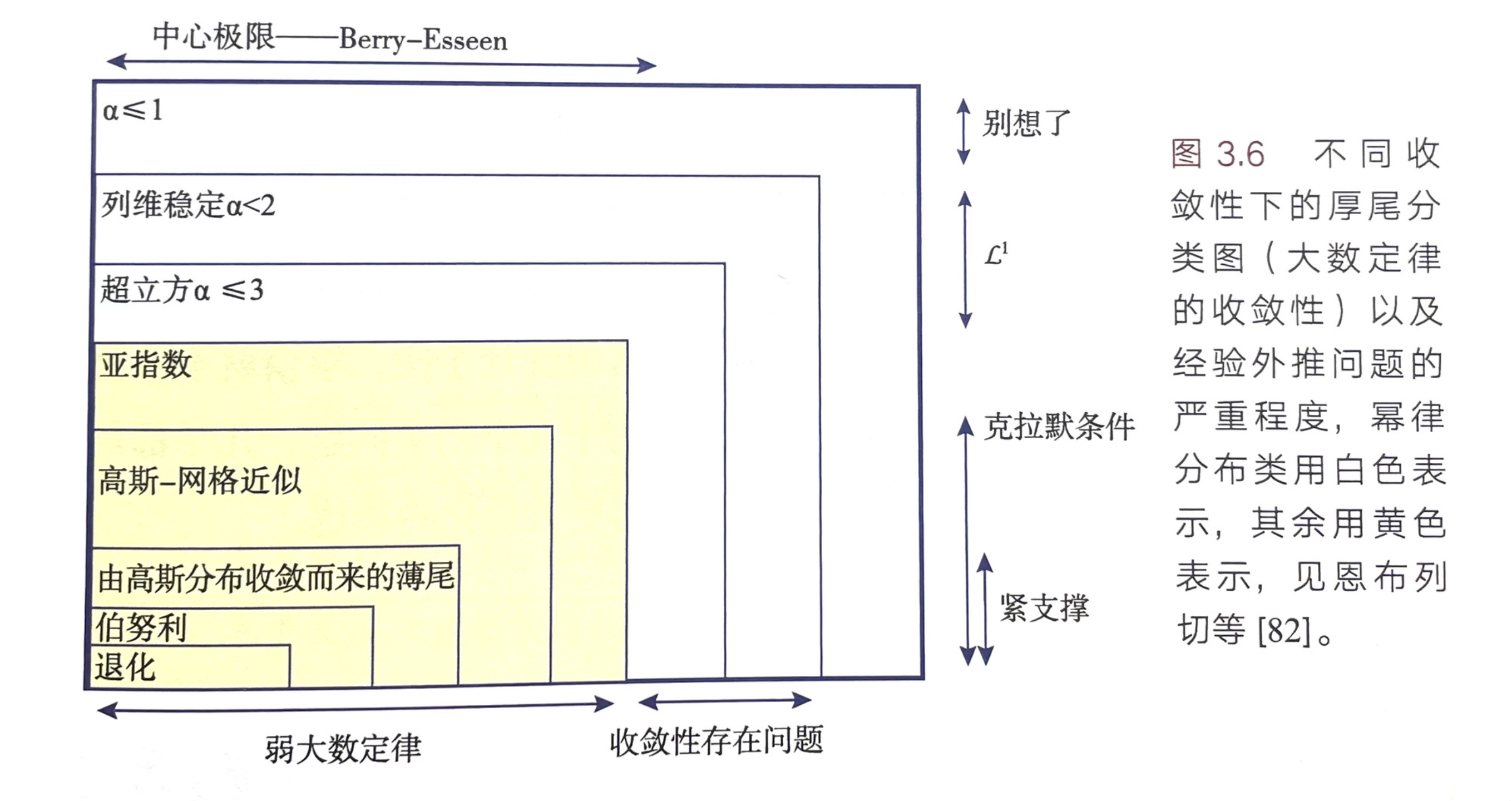
大数定律：当n趋于无穷时，n个独立同分布随机变量取平均值收敛于分布均值。这里收敛的模式有两种，一种是以分布形式收敛，对应弱大数定律，另一种是必然收敛，对应强大数定律。

中心极限定理：在二阶矩（方差）有限的情况下，n 个独立随机变量的和最终会逼近正态分布。

00:56:46 大数定律与中心极限定理的区别

（四）肥尾指标 Kappa

00:59:27 Kappa 值

一般人们在比较肥尾程度时会采用高阶矩，比如峰度（如果存在的话），用其超过某个值的概率作为指标（尺度调整后），但是对于峰度不存在的极度厚尾则无能为力。因此书中提出了一个考量在给定分布下额外数据能在多大程度上增加均值观测的稳定性的肥尾指标κ (Kappa)，主要用于定量衡量大数定律下不同分布收敛的速度（节选自戴国晨《肥尾效应》专栏笔记之上篇)）

（五）分布的不对称性与极端值

01:01:59 如果看到一个 20 倍标准差的事件，我们可以直接排除薄尾分布（书 3.5 章节）

（六）中数定律

01:03:27 中数定律是大数定律和中心极限定理的渐进版本

01:05:32 标普 500 指数的回报率服从幂律分布

如果分布的峰度存在，随着数据量的增加（时间尺度的延长），最终数据会收敛于正态分布。但是随着数据量的增加，我们并没有看到峰度的显著下降，月收益率的峰度不显著低于日峰度。因此，认定标普 500 指数的回报率服从幂律分布（书 10.2 章节）。

（七）期权定价

01:08:59 期权 BSM 假设前提过于理想，包括（节选自书第二十章【金融理论在期权定价上的缺陷】）：

- 假定交易者可以在无摩擦的市场中买卖，且不产生交易成本

- 不考虑订单流对市场价格的影响——如果交易者出售一定数量的股票，后续价格与其完全无关

- 交易者清楚地知道市场的概率分布为正态分布，且参数不具备时变性（所有参数都保持不变）

- 最重要的限制是，市场价格不存在跳跃（也就是跳空高开、低开）

01:11:05 动态对冲无法完全对冲掉期权的所有风险

01:11:53 巴舍利耶模型是假设条件更宽松、鲁棒性更强的期权定价模型（书 22.4.1 章节）

四、补充几个有趣的例子

（一）肥尾变量 vs 薄尾变量

01:12:34 永远不该比较由尾部驱动的随机变量（如流行病）和由躯干驱动的随机变量（如在游泳池中溺水的人数）。

类似的，书中 3.6 章节提到了，不应该把埃博拉病毒和从梯子上跌落进行对比，因为前者有倍增效应，可能会带来很大的系统性风险。比较厚尾变量和薄尾变量的这类错误这被塔勒布称为“幼稚的经验主义”。

（二）预测准确率 vs 赔付

01:15:56 成为正确的预言家不代表会成为富有的人。

人们往往会关注自己的正确率而非赔付，但实际上应该给予赔付更高的关注。因为如果犯错的成本足够低，就可以经常犯错，只要收益是凸性的，也即当他正确的时候会获得很大的收益。反过来说，也可能会在预测的准确率达到 99.9%的情况下破产——2008-2009 年金融危机期间，破产的基金恰恰是那些之前业绩无可挑剔的基金（书 3.4.1 章节）。

（三）与史蒂芬·平克的争论

01:16:50 与史蒂芬·平克的争论（书第十六章之后的 G 章节【第三次世界大战发生的概率有多高？】）

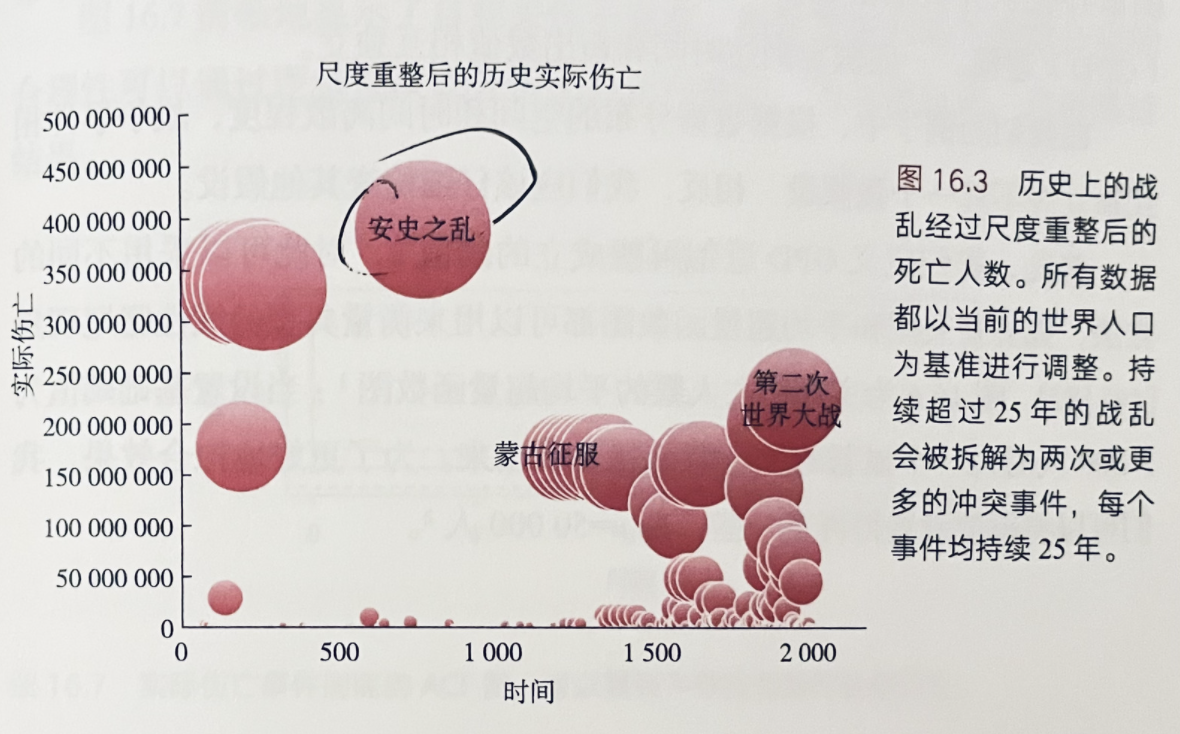
著名认知语言学家史蒂芬·平克，代表作为《人性中的善良天使》《当下的启蒙》。他认为我们正处于人类最和平的时代，人类的历史确有进步可言，我们正生活在有史以来最和平的年代；继而又提出了暴力下降作为度量这种“历史进步”的尺度。

塔勒布认为他只关注频率而不考虑量级。从最近的数据变化中得出结论/归纳出结论并不可行，除非满足一定的置信度条件，这就需要在厚尾条件下有更多的数据。因此，根据最近一年或十年的非自然死亡人数的下降，得出“暴力致死行为有所下降”的结论并不科学。

01:18:10 包括安史之乱等著名战役的实际伤亡统计（书 16.4 章节） 01:21:40 回应 H.T.巴克尔（书第十六章之后的 G 章节【第三次世界大战发生的概率有多高？】）

五、关于黑天鹅

（一）黑天鹅的定义

01:23:22 黑天鹅与肥尾的关系

01:24:58 黑天鹅的核心并非频繁出现，而是单次出现的影响极其巨大

（二）我们应该如何应对黑天鹅

01:25:14 如何应对黑天鹅？

01:26:49 反脆弱 vs 坚固

01:28:01 如何在金融市场上获得反脆弱性？

01:28:50 改变赔付结构

01:29:38 杠铃式配置结构

01:32:19 做多四阶矩

01:33:50 核心不是去预测，而是准备好结构，拥抱黑天鹅的到来

          

六、其他

（一）这本书与塔勒布其他代表作之间的关系

01:34:13 与塔勒布其他代表作之间的关系

（二）关于塔勒布本人的性格

01:36:31 塔勒布本人是什么样的

【相关链接】

1. 《肥尾效应》书评 by 许哲)，是国内最早的权威解读，推荐阅读。2.《戴国晨专栏|塔勒布量化开篇之作《肥尾分布的统计效应》（分为上、下两篇），这个专栏把书中的精华内容用文字形式几乎都提取出来了，推荐阅读，链接如下：

- 上篇)

- 下篇)

3. 本书英文版)，可以与中文版对照阅读。

4. 友台《特许金融街》在本期节目之前也请到了戴国晨做客，更加宏观地聊了聊这本书以及塔勒布相关的内容：https://www.xiaoyuzhoufm.com/episode/62fc4ce2e9685e17002ecd5e

5. 正态分布的68–95–99.7法則维基百科条目)

6. 「矩有四子」重建黑天鹅世界的数学直觉)

7. 概率论中，「矩」（moment）的实际含义是什么？高阶矩表示数据的哪些状态？)

8. 如果大数定律失效，机器学习还能学吗？幂律分布可以告诉你答案)

9. 塔勒布推荐阅读的65本书：https://www.goodbooks.io/people/nassim-nicholas-taleb)

          

剪辑：Sarah

BGM：https://xiazai.51miz.com/sound/266481.html [No Copyright Music]